SubCollectionOf
- Directed
yes
- Source end
- Allowed
- Multiplicity
1 - 1
- Target end
- Allowed
- Multiplicity
1 - 1
- Binary properties
- Reflexivity
no
- Transitivity
yes
- Symmetry
no
- Cyclicity
no
Definition
«SubCollectionOf» is a parthood relation between two collectives. Examples include:
the north part of the Black Forest is part of the Black Forest;
the collection of Jokers in a deck of cards is part of that deck of cards;
the collection of forks in cutlery set is part of that cutlery set;
the collection of male individuals in a crowd is part of that crowd.
The subCollectionOf relation can be shareable in some cases while non-shareable in others. For example, the Kulik siblings is a collection of three members: Marie, Vaclav, and Karel. The same Kulik siblings are sub-collection of the Kulik family, as well as a sub-collection of the FC Bilsko football team, as well as a sub-collection of the Voluntary Firefighter Unit in Bilsko. On contrary, the local organization of the Agrarian Party in Borovno is a sub-collection of the Agrarian Party, but must not be a sub-collection of any other political party, because the statutes prohibit it. «Collective» is a type of collections (and collections are instances of collectives). Collection is an integral whole, or closure defined by a unifying relation. Closure means that no more parts or members can be added to the collection by its unifying relation.
Unlike «Quantity», «Collective» have members and their members may not be placed together (or connected topologically), but unified intentionally e.g. by the common role, or purpose, or social connection. Closure of the unifying relation makes the collective maximal, e.g. the football team is made up of all its members and no subset of its members can make up the same team. For this reason, the «SubQuantityOf» relation is irreflexive. Moreover, for the same reason, any super-collective can have at maximum one sub-collective of a given type. Finally, since every sub-collective of a super-collective is obtained by refining the unifying relation of the latter, the subCollectionOf relation is always transitive. Since collections are maximal, the «SubCollectionOf» parthood must have a cardinality constraint of one and exactly one in the sub-collection side. Addition or removal of a sub-collection (or even a member) of a collection may or may not change identity of the collection. E.g. new firefighter units are taken in the National Rescue System and some of the existing units cease to exist without changing identity of the National Rescue System. Similarly, the Voluntary Firefighter Unit in Karlik consists of three members: Velebil, Strasirybka, and Jech. Then Veselik applies for membership and is taken in the firefighter unit. It is still the same unit, its identity does not change. On contrary, imagine: Jarmila and Jaroslav are spouses. If Jaroslav died, the spousal will cease to exist. And the unifying relation of spousal does not even admit changing Jaroslav for Karel – such a change would change the identity of the spousal, as well. This means that collectives are not extensional (but intentional). That is why only the weak supplementation axiom holds for the subCollectionOf relation (unlike the «SubQuantityOf» relation, where the strong supplementation axiom holds). This axiom means among others that every super-collection must have at least two different types of sub-collections.
Constraints
C1: The classes connected to both association ends of this relation must represent universals whose instances are collectives. Collectives are types as defined in the overview table above.
C2: The maximum cardinality constraint in the association end connected to the part must be one.
Common questions
Ask us some question if something is not clear …
Examples
EX1: 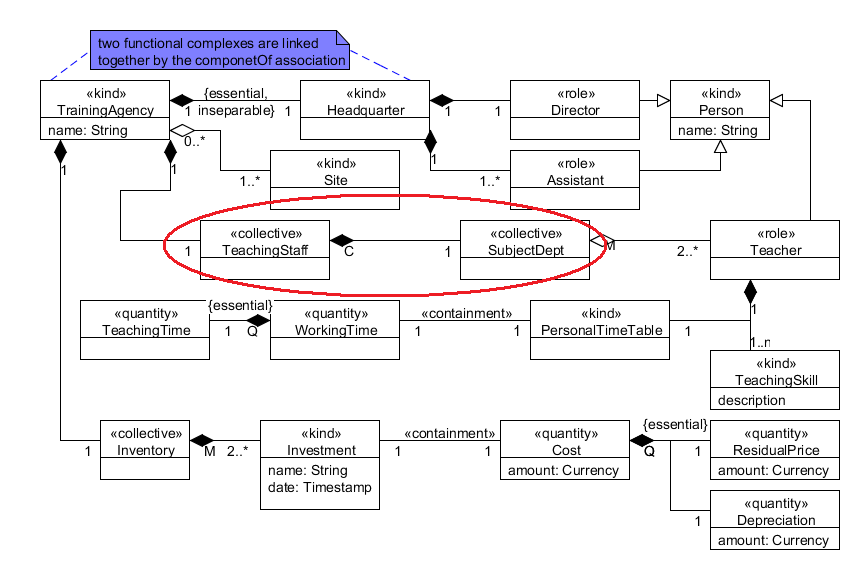
See also
Quoted from:
GUIZZARDI, Giancarlo. Ontological Foundations for Structural Conceptual Models. Enschede: CTIT, Telematica Instituut, 2005. GUIZZARDI, Giancarlo. Introduction to Ontological Engineering. [presentation] Prague: Prague University of Economics, 2011.